Sistem bilangan Real : Garis Bilangan dan Pertidaksamaan
Sistem bilangan Real : Garis Bilangan dan Pertidaksamaan - Pada Bab ini memuat materi dasar yang diperlukan dalam mempelajari kalkulus, beberapa materi yang disampaikan hanyalah merupakan review di masa SMA, namun demikian ada pula beberapa yang relative masih baru, dan akan sedikit memberikan konsep yang lebih mendalam kepada para pembaca.
Materi Yang Dipelajari dalam Sistem Bilangan Real
1.1. Penjelasan Sistem Bilangan Real
1.2. Sifat Sifat Sistem Bilangan Real
1.6. Nilai Mutlak (Absolute Value)
1.7. Selang (Interval)
1.4 Garis Bilangan
Secara geometris, sistem bilangan real R dapat digambarkan
dengan garis lurus. Mula-mula diambil sebarang titik untuk dipasangkan dengan
bilangan 0. Titik ini dinamakan titik asal (origin), ditulis dengan O. Pada
kedua sisi dari O dibuat skala sama (segmen) dan disepakati arah positif
disebelah kanan O, sedangkan arah negatif disebelah kiri O. Selanjutnya,
bilangan-bilangan bulat positif 1, 2, 3, .... dapat dipasangkan dengan
masing-masing titik di kanan O dan bilangan-bilangan -1,-2,-3,... dengan
titik-titik di sebelah kiri O. Dengan membagi setiap segmen, maka dapat
ditentukan lokasi untuk bilangan-bilangan ½, -2/3, √2 dst. Perhatikan Gambar
dibawah ini.
Dengan cara demikian, maka setiap bilangan real menentukan
tepat satu titik pada garis lurus dan sebaliknya setiap titik pada garis lurus
menentukan tepat satu bilangan real. Oleh sebab itu, garis lurus sering disebut
pula Garis Bilangan Real.
1.5 Pertidaksamaan
Perubah (variable) adalah lambang (symbol) yang digunakan
untuk menyatakan sebarang anggota suatu himpunan. Jika himpunannya R maka
perubahnya disebut perubah real. Selanjutnya, yang dimaksudkan dengan perubah
adalah perubah real. Pertidaksamaan (inequality) adalah pernyataan matematis
yang memuat satu perubah atau lebih dan salah satu tanda ketidaksamaan (<,
>, ≤, ≥).
Contoh Soal
a. 2x – 7 ≤ x + 1
b. ( (2x-1)/(x+3) ) > 1
c. x2 + y2 ≤ 9
d. x2 – x – 12 < 0
Menyelesaikan suatu pertidaksamaan memiliki arti mencari
seluruh bilangan real yang dapat dicapai oleh perubah-perubah yang ada dalam
pertidaksamaan tersebut sehingga pertidaksamaan tersebut menjadi benar.Himpunan
semua bilangan yang demikian ini disebut penyelesaian. Sifat-sifat dan hukum
dalam R sangat membantu dalam mencari penyelesaian suatu pertidaksamaan.
Contob 1.1.2 Tentukan penyelesaian pertidaksamaan 2x – 5
< 5x + 7
Penyelesalan:
ó2x
– 5 < 5x + 7
ó2x
– 5 – 5x + 5 < 5x + 7 – 5x + 5
ó
-3x < 12
ó
-3x(-1/3) > 12.(-1/3)
ó
x > -4
Jadi, penyelesaian pertidaksamaan di atas adalah {x ∈
R| x > -4}
Pertidaksamaan tipe lain mungkin lebih sulit diselesaikan
dibandingkan pertidaksamaan- pertidaksamaan seperti pada contoh di atas.
Beberapa contoh diberikan sebagai berikut:
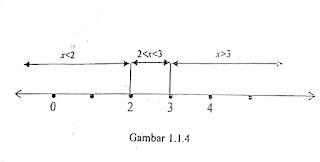
Penyelesaian pertidaksamaan di atas dapat pula diterangkan sebagai berikut: ruas kiri pertidaksamaan bermilai nol jika x = 2 atau x = 3 . Selanjutnya, ke dua bilangan ini membagi garis bilangan menjadi 3 bagian: x < 2, 2 < x < 3, dan x > 3(Gambar 1.1.4).
Contoh 1.1.3 Tentukan penyelesaian pertidaksamaan: x – 5x +
6 > 0.
Penyelesaian: Dengan memfaktorkan nuas kiri pertidaksamaan,
maka diperoleh:
(x – 2)(x – 3) > 0
Telah diketahui bahwa hasil kali 2 bilangan real positif
apabila ke dua faktor positif atau ke dua faktor negatif. Oleh karena itu,
(i) Jika ke dua faktor positif maka:
x – 2 > 0 dan x – 3 > 0
óx
> 2 dan x > 3
Sehingga diperoleh: x > 3
(ii) Jika ke dua faktor negatif, maka:
x – 2 < 0 dan x – 3 < 0
ó
x < 2 dan x < 3
Diperoleh: x < 2
Jadi, penyelesaian adalah {x ∈ R| x < 2 atau x > 3}
Penyelesaian pertidaksamaan di atas dapat pula diterangkan sebagai berikut: ruas kiri pertidaksamaan bermilai nol jika x = 2 atau x = 3 . Selanjutnya, ke dua bilangan ini membagi garis bilangan menjadi 3 bagian: x < 2, 2 < x < 3, dan x > 3(Gambar 1.1.4).
Pada bagian x < 2, nilai (x – 2) dan (x – 3) keduanya
negatif, sehingga hasil kali keduanya positif. Pada segmen 2 < x < 3, (x –
2)bernilai positif sedangkan (x – 3) bernilai negatif. Akibatnya, hasil kali
keduanya bernilai negatif. Terakhir, pada bagian x > 3, (x – 2) dan (x – 3) masing-masing
bernilai positif sehingga hasil kali keduanya juga positif. Rangkuman uraian di
atas dapat dilihat pada Tabel 1.1.1 di bawah ini.
Tanda Nilai
|
Kesimpulan
|
|||
(x – 2)
|
(x – 3)
|
(x – 2) (x – 3)
|
||
x < 2
|
-
|
-
|
+
|
Pertidaksamaan
Dipenuhi
|
2 < x < 3
|
+
|
-
|
-
|
Pertidaksamaan
Tidak Dipenuhi
|
x > 3
|
+
|
+
|
+
|
Pertidaksamaan
Dipenuhi
|
Jadi, penyelesaian pertidaksamaan adalah {x ∈ R| x < 2 atau x > 3}
Metode penyelesaian seperti pada Contoh 1.1.3 di atas dapat
pula diterapkan pada bentuk-bentuk pertidaksamaan yang memuat lebih dari 2
faktor maupun bentuk-bentuk pecahan.
Contoh 1.1.4 Tentukan penyelesaian x3 – 2x2
– x + 1 ≤ -1
Penyelesaian: Apabila ke dua ruas pada pertidaksamaan di
atas ditambahi 1, maka diperoleh:
x3 – 2x2 – x + 2 ≤ 0
ó(x
- 1)(x + 1)(x – 2) ≤ 0
Jika (x – 1)(x + 1)(x – 2) = 0 maka diperoleh: x = -1, x = 1,
atau x = 2. Selanjutnya, perhatikan table
maka diperoleh: x = -1, x = 1,
atau x = 2. Selanjutnya, perhatikan table
Berikut :
Tanda Nilai
|
Kesimpulan
|
||||
(x
+ 1)
|
(x
- 1)
|
(x
– 2)
|
(x – 1)(x + 1)(x – 2)
|
||
x < -1
|
-
|
-
|
-
|
-
|
Pertidaksamaan
Dipenuhi
|
-1
< x < 1
|
+
|
-
|
-
|
+
|
Pertidaksamaan
Tidak Dipenuhi
|
1 < x < 2
|
+
|
+
|
-
|
-
|
Pertidaksamaan
Dipenuhi
|
x > 2
|
+
|
+
|
+
|
+
|
Pertidaksamaan
Tidak Dipenuhi
|
x = -1
|
0
|
-2
|
-3
|
0
|
Pertidaksamaan
Dipenuhi
|
x = 1
|
2
|
0
|
-1
|
0
|
Pertidaksamaan
Dipenuhi
|
x = 2
|
3
|
1
|
0
|
0
|
Pertidaksamaan
Dipenuhi
|
Jadi, penyelesaian adalah x ∈ R| x ≤ -1 atau 1 ≤ x ≤ 2}}
Contoh Selesaikan ( (2x + 6)/(x – 2) ) ≤ x + 1
Penyelesaian: Apabila pada ke dua ruas ditambahkan –(x + 1) maka diperoleh:
( (2x + 6)/(x – 2) ) -
x + 1 ≤ 0
ó(
(2x + 8 – x2 + x + 2)/(x – 2) ) ≤ 0
ó
( (x2 – 3x – 10)/(x – 2) ) ≥ 0
ó
( (x – 5)(x + 2)/(x – 2) ) ≥ 0
Nilai nol pembilang adalah -2 dan 5, sedangkan nilai nol
penyebut adalah 2. Sekarang, untuk mendapatkan nilai x sehingga (
(x – 5)(x + 2)/(x – 2) ) ≥ 0 diperhatikan tabel berikut:
Tanda Nilai
|
Kesimpulan
|
||||
(x – 5)
|
(x + 2)
|
(x – 2)
|
( (x – 5)(x + 2)/(x –
2) ) ≥ 0
|
||
x < -2
|
-
|
-
|
-
|
-
|
Pertidaksamaan
Tidak Dipenuhi
|
-2 < x < 2
|
+
|
-
|
-
|
+
|
Pertidaksamaan
Dipenuhi
|
2 < x < 5
|
+
|
+
|
-
|
-
|
Pertidaksamaan
Tidak Dipenuhi
|
x > 5
|
+
|
+
|
+
|
+
|
Pertidaksamaan
Dipenuhi
|
x = - 2
|
0
|
-4
|
-7
|
0
|
Pertidaksamaan
Dipenuhi
|
x = 2
|
4
|
0
|
-3
|
Tidak
Terdefinisi
|
Pertidaksamaan
Tidak Dipenuhi
|
x = 5
|
7
|
3
|
0
|
0
|
Pertidaksamaan
Dipenuhi
|
Jadi, penyelesaian adalah {x ∈ R| x ≥ 5 atau -2 ≤ x < 2}}
Itu saja yang dapat saya jelaskan mengenai Sistem Bilangan Real Sub Bab Garis Bilangan dan Pertidaksamaan. Semoga dengan adanya materi yang kami ajarkan dapat membantu sobat untuk lebih mengerti konsep konsep dalam mempelajari kalkulus ini. Jika kurang paham bisa kalian tanyakan di kolom komentar.
Sistem bilangan Real : Garis Bilangan dan Pertidaksamaan
4/
5
Oleh
zedukasi



EmoticonEmoticon