Nilai Mutlak dan Selang Interval Dalam Sistem Bilangan Real
Nilai Mutlak dan Selang Interval dalam sistem bilangan real - Pada Bab ini memuat materi dasar yang diperlukan dalam mempelajari kalkulus, beberapa materi yang disampaikan hanyalah merupakan review di masa SMA, namun demikian ada pula beberapa yang relative masih baru, dan akan sedikit memberikan konsep yang lebih mendalam kepada para pembaca. Nah pada artikel kali ini saya akan menekankan pembahasan mengenai Nilai Mutlak dan Selang Interval.
Materi Yang Dipelajari dalam Sistem Bilangan Real
1.1. Penjelasan Sistem Bilangan Real
1.2. Sifat Sifat Sistem Bilangan Real
1.3. Relasi Urutan
1.4. Garis Bilangan
1.4. Garis Bilangan
1.5. Pertidaksamaan
1.6 Nilai Mutlak (Absolute Value)
Nilai mutlak suatu bilangan adalah panjang/jarak bilangan tersebu: dari bilangan 0. Jadi, mutlak 5 adalah 5, nilai mutlak -7 adalah 7, nilai mutlak 0 adalah 0, dan seterusnya.Definisi 1.1.6 Nilai mutlak x ∈ R, ditulis dengan notasi |x|, didefinisikan sebagai:
Nilai mutlak suatu bilangan adalah panjang/jarak bilangan tersebu: dari bilangan 0. Jadi, mutlak 5 adalah 5, nilai mutlak -7 adalah 7, nilai mutlak 0 adalah 0, dan seterusnya.
Definisi Nilai Mutlak
Definisi 1.1.6 Nilai mutlak x ∈ R, ditulis dengan notasi |x|, didefinisikan sebagai:|x| = √x2
Definisi di atas dapat pula dinyatakan sebagai:
|x| = {x, jk x ≥ 0 -x, jk x < 0 atau
NB : Untuk menghindari kesalahan dalam mengerjakan Soal Nilai Mutlak akan lebih baik menggunakaan definisi dalam pengerjaan soal.
|x| = {x, jk x ≥ 0 -x, jk x < 0 atau
Saya akan memberi contoh pengerjaan yang hanya bisa dikerjakan dengan definisi mutlak. untuk itu tunggu saja, dan maaf karena tidak bisa segera karena kesibukan saya di dunia nyata sebagai seorang mahasiswa.
Jika kalian ingin menanyakan sesuatu bisa kalian komentar atau melalui contact form blog atau email saya. Jika tidak sibuk saya akan baca dan mengerjakan soal yang kalian berikan terimakasih. Kami bekerja menjadi tim.
Sebagai contoh, |-8| = -(-8) = 8, |5/2|=5/2,|3|=3 dst. Selanjutnya, sifat-sifat nilai mutlak diterangkan sebagai berikut.
|3x| = 5 ó3x = 5 atau 3x = -5
óx = 5/3 ∨ x = -5/3
Secara sama,
|2x - 3| = 7 berarti 2x - 3 = 7 atau 2x - 3 = -7
ó 2x = 10 atau 2x = -4
ó x = 5 atau x = -2
Sifat Sifat Nilai Mutlak 1.1.9 Jika a ≥ 0, maka:
(a) |x| ≤ a ó -a ≤ x ≤ a(b) |x| ≥ a ó x ≤ -a atau x ≥ a.
Contoh Soal Nilai Mutlak 1.1.10 Selesaikan 2x - 3 ≥ 7.
Penyelesaian: Menggunakan Sifat 1.1.9 (b), diperoleh:
|2x-3| ≥ 27 ó (2x - 3) ≤ 7 atau (2x - 3) ≥ 7
ó 2x ≤ -4 atau 2x ≥ 10
ó x ≤ -2 atau x ≥ 5
Jadi, penyelesaian adalah {x ∈ R|x ≤ -2 atau x ≥ 5}
Contoh Soal Nilai Mutlak 1.1.11 Tentukan semua nilai x sehingga |2x/(x - 2)| ≤ 3
Penyelesaian: Berdasarkan Sifat 1.1.9 (a), maka:
|2x/(x - 2)| ≤ 3ó -3 ≤ 2x/(x - 2) ≤ 3
ó 2x/(x - 2) ≥ -3 dan 2x/(x - 2) ≤ 3
Selanjutnya, kita kaan menyelesaikan keduanya tersebut dengan cara pertidaksamaan.
- Untuk 2x/(x-2) ≥ -3
ó 2x/(x-2) + 3 ≥ 0
ó 2x/(x - 2) + (3x - 6)/(x - 2) ≥ 0
ó (5x - 6)/(x - 2) ≥ 0
untuk (5x - 6) => x ≥ 6/5 atau x ≤ 6/5
untuk (x - 2) => x > 2 atau x < 2 Karena x ≠ 2
Menggunkaan tabel
|
Tanda Nilai
|
||||
|
5x - 6
|
x - 2
|
(5x - 6)/(x - 2)
|
||
|
x > 2
|
+
|
+
|
+
|
Pertidaksamaan Memenuhi
|
|
6/5 ≤ x < 2
|
+
|
-
|
-
|
Pertidaksamaan Tidak Memenuhi
|
|
x ≤ 6/5
|
-
|
-
|
+
|
Pertidaksamaan Memenuhi
|
|
2
|
4
|
0
|
Tidak Memenuhi
|
Pertidaksamaan Tidak Memenuhi
|
|
6/5
|
0
|
4/5
|
0
|
Pertidaksamaan Memenuhi
|
- Untuk 2x/(x-2) ≤ 3
ó 2x/(x-2) - 3 ≤ 0
ó 2x/(x - 2) - (3x - 6)/(x - 2) ≤ 0
ó (-x + 6)/(x - 2) ≤ 0
untuk (-x + 6) => x ≥ 6 atau x ≤ 6
untuk (x - 2) => x > 2 atau x < 2 Karena x ≠ 2
Menggunkaan tabel
|
Tanda Nilai
|
||||
|
-x + 6
|
x - 2
|
(-x + 6)/(x - 2)
|
||
|
x ≥ 6
|
-
|
+
|
-
|
Pertidaksamaan Memenuhi
|
|
2 < x ≤ 6
|
+
|
+
|
+
|
Pertidaksamaan Tidak Memenuhi
|
|
x < 2
|
+
|
-
|
-
|
Pertidaksamaan Memenuhi
|
|
2
|
4
|
0
|
Tidak Memenuhi
|
Pertidaksamaan Tidak Memenuhi
|
|
6
|
0
|
4
|
0
|
Pertidaksamaan Memenuhi
|
Hp1 dan Hp2 = {x ∈ R|x < 6/5 atau x ≥ 6}
Sifat Sifat Nilai Mutlak 1.1.7 Jika x,y ∈ R maka:
a. |x| ≥ 0 |x| = 0 x = 0b. |x.y| = |x|.|y| |x/y| = |x/y|, asal y ≠ 0
c. ||x| - |y|| ≤ |x + y| ≤ |x| + |y| (ketaksamaan segitiga)
||x| - |y|| ≤ |x - y| ≤ |x| + |y|
Secara geometris, nilai mutlak |x - a| dapat diartikan sebagai jarak dari a ke x. Sebagai contoh, jika
|x - 3| = 7 maka artinya x berjarak 7 unit di sebelah kanan atau di sebe lah kiri 3 (lihat Gambar 1.1.5).
Jadi, penyelesaian|x - 3| = 7 adalah {-4,10}
Dengan mengingat Sifat 1.1.7 (b), kiranya mudah dipahami sifat berikut:
Sifat 1.1.8 Jika a ≥ 0,maka: |x| = a ó x = a atau x = -a
Sebagai contoh,
|x| = 4 berarti x = 4 atau x = -4
Contoh 1.1.12 Tentukan penyelesaian pertidaksamaan |x - 4| > x - 2
Penyelesaian:
(i). Apabila x - 2 < 0. maka selalu berlaku |x - 4| > x -2 untuk setiap x. Sehingga diperoleh: x < 2
(ii). Jika x - 2 ≥ 0 maka:
|x - 4| > x - 2
ó {(x - 4) < -(x - 2) atau (x - 4) > (x -2)}, x ≥ 2
ó 2x< 6, x≥2
ó 2≤x<3
Dari (i) dan (ii), diperoleh x < 3
Contoh 1.1.12 Tentukan penyelesaian pertidaksamaan |x - 4| > x - 2
Atau penyelesaian dengan cara definisi Dari soal Contoh 1.1.12 ini |x - 4| > x - 2
|x - 4| {(x - 4), jk x ≥ 4 ATAU (-x + 4), jk x < 4
(a) Untuk x ≥ 0, Maka
x - 4 > x - 2
-2 > 0 (Tidak Memenuhi)
(b) Untuk x < 4
-x + 4 > x - 2
-2x > -6
x < 3
Maka Penyelesaian (a) dan (b) diperoleh Hp = {x ∈ R|x <3}
1.7 Selang (Interval)
Diberikan sebarang dua bilangan real a dan b, dengan a < b. Berturut-turut didefinisikan:[a, b]={ x| a ≤ x ≤ b} ,
[a, b)={x| a ≤ x < b},
[a, ∞)={x| x ≥ a}
(-∞, a]={x| x ≤ a}
(a, b)={x| a < x < b} ,
(a, b]={x| a < x ≤ b} ,
(a, ∞)={x| x > a} ,
(-∞, a)={x| x < a} ,
Demikian penjelasan mengenai Nilai Mutlak dan Selang Interval semoga dengan materi yang kami berikan dapat membantu pengerjaan soal kalian. Saya sarankan dalam mengunakan sifat sifat nilai mutlak kita harus terlebih dahulu tahu keduanya harus positif, jika terjadi negatif maka sifat tidak dapat digunakan. Maka dari itu saya saranakan dalam pengerjaan soal menggunakan Definisi Mutlak. Itu saja Semoga dapat membantu kalian dan semoga sukses.
Nilai Mutlak dan Selang Interval Dalam Sistem Bilangan Real
4/
5
Oleh
zedukasi
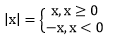



EmoticonEmoticon