Contoh Soal Cara Menentukan Titik Stasioner dan Jenis-Jenisnya
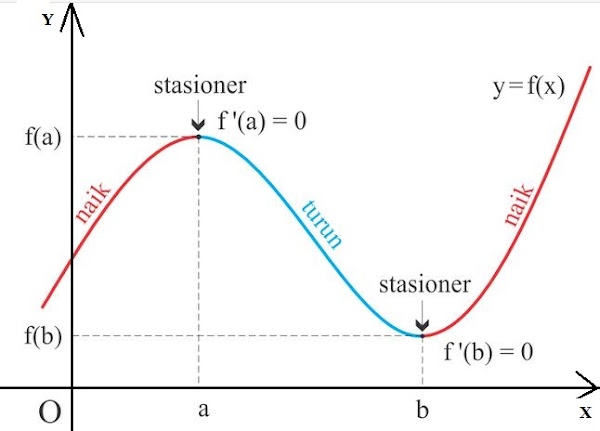
Pada kesempatan kali ini kita omahjenius akan berbagi mengenai Soal dan Pembahasan Menentukan Titik Stasioner. Jika fungsi y = f(x) diferensiabel di x = a dengan f'(a) = 0, maka f(a) adalah nilai stasioner dari fungsi f(x) di x = a.
Untuk itu simak terus pembahasan dari kami, semoga membantu kalian belajar. SEMANGATT!!!
3 Jenis Nilai Stasioner
Terdapat 3 jenis nilai stasioner, yaitu:
1. Nilai Balik Maksimum
2. Nilai Balik Minimum
3. Titik Belok
Contoh Soal & Pembahasan Titik Stasioner
Soal 1
Jika x₁ dan x₂ merupakan akar persamaan x² - (a -1)x + a = 0.
Nilai stasioner dari x₁³ + 3x₁.x₂ + x₂³ dicapai untuk a = .....
A. 1 dan 2
B. 1 dan 3
C. 2 dan 3
D. -1
E. 0, -1 dan 1
Pembahasan:
x² - (a -1)x + a = 0
a = 1, b = -(a - 1), c = a
x₁ + x₂ = -b/a = (a - 1)
x₁.x₂ = c/a = a
x₁³ + 3x₁.x₂ + x₂³ = x₁³+ x₂³+ 3x₁.x₂
= (x₁ + x₂)³ - 3x₁.x₂(x₁ + x₂) + 3x₁.x₂
= (a - 1)³ - 3a(a - 1) + 3a
= (a - 1)³ - 3a² + 6a
Stasioner <=> turunan pertama = 0
<=> 3(a - 1)² - 6a + 6 = 0
<=> (a - 1)² - 2a + 2 = 0
<=> a² - 2a +1 - 2a + 2 = 0
<=> a² - 4a + 3 = 0
<=> (a - 1)(a - 3) = 0
<=> a = 1 atau a = 3
(JAWABAN: B)
Soal 2
Fungsi y = 4x³ - 18x² + 15x - 20 mencapai maksimum untuk nilai x = .....
A. 0,5
B. 1,5
C. 2
D. 2,5
E. 3
Pembahasan:
y = 4x³ - 18x² + 15x - 20
Stasioner <=> y' = 0
y' = 12x² - 36x + 15 = 0
<=> 3(4x² - 9x + 5) = 0
<=> 3(2x - 1)(2x - 5) = 0
<=> x = ½ atau x = 5/2
Jadi, fungsi y mencapai maksimum untuk x = ½.
(JAWABAN: A)
Soal 3
Titik belok dari fungsi y = x³ + 6x² + 9x + 7 adalah .....
A. (-2,3)
B. (-2,7)
C. (-2,5)
D. (2,5)
E. (2,10)
Pembahasan:
y = x³ + 6x² + 9x + 7
y' = 3x² + 12x + 9
y" = 6x + 12
Titik belok <=> y" = 0
6x + 12 = 0
<=> 6x = -12
<=> x = -12/6
<=> x = -2
Subtitusi nilai x = -2 ke fungsi y.
y = (-2)³ + 6(-2)² + 9(-2) + 7
= -8 + 24 - 18 + 7
= 5
Jadi, titik belok dari fungsi y adalah (-2,5)
(JAWABAN: C)
Soal 4
y = x³ -3x² -24x - 7 maka nilai stasionernya adalah .....
A. -2 dan 4
B. -35
C. 1
D. 21 dan -87
E. 1,21 dan -77
Pembahasan:
y = x³ -3x² -24x - 7
Stasioner <=> y' = 0
y' = 3x² - 6x - 24 = 0
<=> x² - 2x - 8 = 0
<=> (x - 4)(x + 2) = 0
<=> x = 4 atau x = -2
Fungsi maksimum pada x = -2,maka nilai balik maksimumnya:
f(-2) = (-2)³ -3(-2)² -24(-2) - 7
= -8 - 12 + 48 - 7
= 21
Fungsi minimum pada x = 4, maka nilai balik minimumnya:
f(4) = (4)³ -3(4)² -24(4) - 7
= 64 - 48 - 96 - 7
= -87
Jadi, nilai stasionernya adalah 21 dan -87.
(JAWABAN: D)
Soal 5
Sebuah titik materi dengan persamaan s(t) = -(⅓)t³ + 3t² -5t (t = waktu, s = kedudukan). Titik materi ini mempunyai kecepatan tertinggi pada saat t = .....
A. 1
B. 2
C. 3
D. 4
E. 5
Pembahasan:
s(t) = -(⅓)t³ + 3t² -5t
v(t) = s'(t)
v(t) = -t² + 6t - 5
v(t) maksimum untuk t = -b/2a = -6/-2 = 3.
(JAWABAN: C)
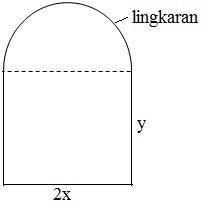
Soal 6
Sebuah pintu berbentuk seperti tergambar. Keliling pintu sama dengan p. Agar luas pintu maksimum, maka x sama dengan .....
A. pπ
B. p - π4
C. p4+π
D. p4 + π
E. p4π
Pembahasan:
Keliling = 2x + 2y + πx = p
<=> 2y = p - 2x - πx
Luas = 2xy + ½ πx²
= x(p - 2x - πx) + ½ πx²
= px - 2x² - πx² + ½ πx²
= px - 2x² - ½ πx²
Syarat Luas maksimum, L' = 0
L' = p - 4x - πx = 0
<=> p - (4 + π)x = 0
<=> x = −p−(4+π)
<=> x = p4+π
(JAWABAN: C)
Soal 7
Selisih dua bilangan adalah 4p. Nilai terkecil dari hasil perkalian kedua bilangan itu adalah .....
A. 6p²
B. 4p²
C. -2p²
D. -4p²
E. -5p²
Pembahasan:
Misalkan bilangan itu adalah x dan y, maka:
y - x = 4p atau y = 4p + x
K = xy = x(4p + x) = 4px + x²
dkdx = 0
4p + 2x = 0
<=> 2x = -4p
<=> x = -2p
Kmin = -2p(4p + (-2p))
= -2p(2p)
= -4p²
(JAWABAN: D)
Itu saja mengenai contoh soal cara memnentukan titik stasioner beserta jenis jenisnya. Jangan lupa selalu belajar. SEMANGATTT
Titik Stasioner || Soal dan Pembahasan Menentukan Titik Stasioner || Jenis-jenis Nilai Stasioner || Titik Belok



EmoticonEmoticon